Answer: C
Solution:
It is best to split 11 hours and 5 minutes into 2 parts, one of 11 hours and another of 5 minutes. We know that there is 60 minutes in a hour. Therefore, there are 11*60 minutes in 11 hours. Adding the second part(the 5 minutes) we get 660+5=665.
中文解析:
11小时5分钟=11*60+5=665分钟. 答案是C.
Answer: A
Solution:
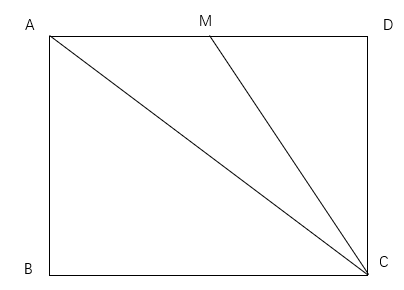
We can find the area of the entire rectangle, DCBA to be 8*6=48 and find DCM area to be 6*4/2=12 and BCA to be 6*8/2=24 48-12-24=12 .
中文解析:
三角形AMC的面积可以使用长方形的面积减去三角形ABC,减去三角形MDC求得. 长方形的面积是8*6=48.
三角形ABC的面积是: 1/2 * 8*6=24. 三角形MDC的面积是: 1/2 * 4*6=12. 因此三角形AMC的面积是: 48-24-12=12. 答案是A.

Answer: A
Solution:
We can call the remaining score r. We also know that the average, 70, thus,(70+80+90+r)/4 =70. =>r=40.
中文解析:
4个人的平均分是70分, 其中80比70多10, 90比70多20, 因此另一个分数应该比70少30分,是40分. 答案是A.

Answer: B
Solution:
When Cheenu was a boy, he could run 15 miles in 3 hours and 30 minutes =3*60+30=210 minutes, thus running 210/15=14 minutes per mile. When he is an old man, he can walk 10 miles in 4 hours =4*60=240 minutes, thus walking 240/10=24 minutes per mile. Therefore it takes him 10 minutes longer to walk a mile now compared to when he was a boy.
中文解析:
Cheenu年轻的时候,速度是15英里每210分钟, 因此1英里需要14分钟. 年老时的速度是10英里每240分钟,则1英里需要24分钟. 时间差是24-14=10 分钟. 答案是B.

Answer: E
Solution:
From the second bullet point, we know that the second digit must be 3. Because there is a remainder of 1 when it is divided by 9, the multiple of 9 must end in a 2. Since 8*9=72;
The number 72+1=73 satisfies both conditions. The remainder of 77/11 is 7.
中文解析:
N被10除的余数是3, 则这个2位数的个位数应该是3. N被9除余数是1, 寻找9的倍数并且个位数是2的2位数,是72. 因此这个数是73. 73除11的余数是7. 答案是E.

Answer: B
Solution:
We first notice that the median name will be the 10th name. The length is 4.
中文解析:
这19个人的名字的长度分别是: 3,3,3,3,3,3,3,4,4,4,5,6,6,6,6,7,7,7,7. 该数列已经是从小到大排列了,因此中位数是第10个. 是4. 答案是B.
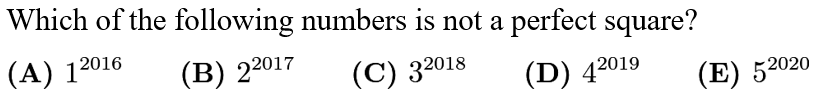
Answer: B
Solution:
We know that our answer must have an odd exponent in order for it to not be a square. Because 4 is a perfect square, 4^2019 is also a perfect square, so our answer must be B.
中文解析:
选项A是1, 是perfect square. 选项C可以写成3的1009次方再平方,是perfect square. 选项D可以写成2的2019次方再平方,是perfect square. 选项E可以写成5的1010次方再平方, 是perfect square, 只有B不是perfect square. 因此答案是B.
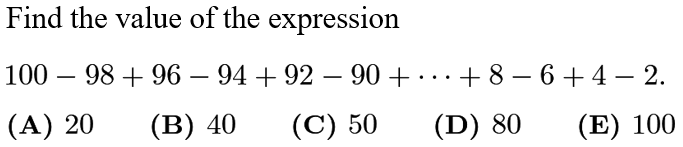
Answer: C
Solution:
We can group each subtracting pair together: (100-98)+(96-94)+(92-90)+…+(8-6)+(4-2)=2+2+…+2+2. There are 50 even numbers, therefore there are 50/2=25 even pairs. Therefore the sum is 2*25=50.
中文解析:
=(100-98)+(96-94)+(92-20)+...+(8-6)+(4-2) . 从1到100 有50个双数, 即25对双数,因此2*25=50. 答案是C.

Answer: B
Solution:
The prime factorization is 2016=2^5*3^2*7. Since the problem is only asking us for the distinct prime factors, we have 2,3,7. Their desired sum is then 12.
中文解析:
找出2016的质因数,分别是: 2,2,2,2,2, 3,3, 7. 互不相同的有2,3,7. 其和是: 2+3+7=12. 答案是B.
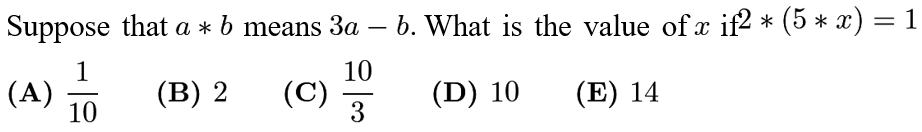
Answer: D
Solution:
Let us plug in (5*x) into 3a-b. Thus it would be 3(5)-x=15-x. Now we have 2*(15-x)=3(2)-(15-x)=6-15+x=x-9. Since 2*(5*x)=1, x-9=1; solving for x we have x=10.
中文解析:
5*x 是15-x. 2*(15-x)的意思是: 6-(15-x)=x-9. 因此 x-9=1, 求出x=10. 答案是D.

Answer: B
Solution:
We can write the two digit number in the form of 10a+b, reverse is 10b+a. The sum of those numbers is: (10a+b)+(10b+a)=132; => a+b=12; We can use brute force to find order pairs (a,b), such that a+b=12. Thus our ordered pairs are(3,9),(3,8),(5,7),(6,6),(7,5),(8,4),(9,3). Totally 7 pairs.
中文解析:
假设这个两位数的十位数是a,个位数是b, 这个数是10a+b; 反过来之后变成了10b+a. 根据题意,和是132,则 (10a+b)+(10b+a)=132; 可得: 11*(a+b)=132, 因此a+b=12. 符合条件的数据有: 39, 48, 57, 66, 75, 84, 93. 共7组. 答案是B.
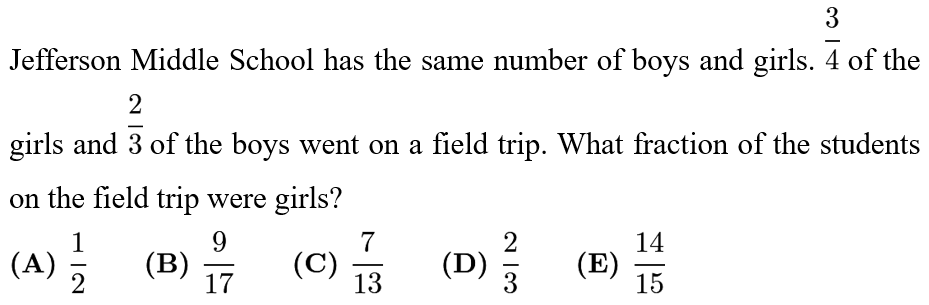
Answer: B
Solution:
Let there be b boys and g girls in the school. We see g=b, which mean (3/4)*b+(2/3)*b=17/12b kids went on the trip and (3/4)b kids are girls. So, the answer is (3/4)/(17/12)=9/17.
中文解析:
男生和女生一样多,假设都是n个. 参加旅行的女生是: 3/4 * n 个, 男生是 2/3 * n个. 注意参加的男生和女生的人数都是整数, 因此n需要是分母4和3的最小公倍数,即12. 则女生是9个,男生是8个. 女生占比: 9/(9+8)=9/17. 答案是B.

Answer: D
Solution:
The product can only be 0 if one of the numbers is 0. Once we chose 0, there are 5 ways we can chose the second number, There are C(6,2) ways we can chose 2 numbers randomly, and that is 15. So, 5/15=1/3 so the answer is 1/3.
中文解析:
两个数的乘积是0, 则第一个数是0或者第二个数是0. 因此本题从这6个数中必须选择一个0, 另外一个数随意. 如果第一个数是0, 概率是1/6. 如果第一个数不是0, 第二个数是0的概率是: 5/6 * 1/5=1/6. 因此本题的概率是1/6 + 1/6=1/3. 答案是D.

Answer: A
Solution:
Since he uses a gallon of gas every 35 miles, he had used 350/35=10 gallons after 350 miles. Therefore, after the first leg of his trip he had 14-10=4 gallons of gas left. Then, he bought 8 gallons of gas, which brought him up to 12 gallons of gas in his gas tank. When he arrived, he had 7 gallons of gas. So he used 5 gallons of gas on the second leg of his trip. Therefore, the second part of his trip covered 5*35=175 miles. Adding this to the 350 miles, we see that he drove 525 miles.
中文解析:
整段行程使用的汽油是从14+8-7=15. 每加仑可行驶35英里, 则15加仑可行使 15*35=525英里. 答案是A.
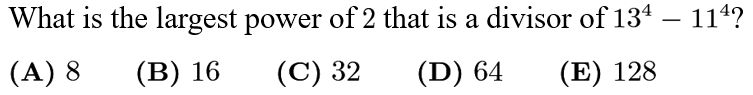
Answer: C
Solution:
First, we use difference of squares on 13^4-11^4=(13^2)^2-(14^2)^2, to get (13^2+11^2)*(13^2-11^2)=(169+121)*(13+11)*(13-11)=290*24*2=(2*5*3*3)*(3*2*2*2)*2=2^5*3*3*3*5=32*3*3*3*5. we see that the greatest power of 2 is 32.
中文解析:
13的4次方减去11的4次方是: 290*48=29*10*3*16=29*5*2*16=29*5*32. 32 是2的5次方. 答案是C.

Answer: D
Solution:
Each lap Bonnie runs, Annie runs another quarter lap, so Bonnie will run four laps before she is overtaken. This means that Annie and Bonnie are equal so that Annie needs to run another lap to overtake Bonnie. That means Annie will have run 5 laps.
中文解析:
A比B的速度快25%,即当B跑100比时, A跑了125米. 当B跑400米时, A多跑了100米, 跑了500米. 起跑后,A和B相遇,需要A比B多跑一圈,即多跑400米. 当B跑1600米时, A多跑了1600* 1/4 =400米, 即此时AB相遇. B跑了1600米,A跑了1600+400=2000米,即5圈时,AB相遇. 答案是D.

Answer: D
Solution:
Counting the prohibited cases, we find that there are 10 of them. This is because we start with 9,1,1 and we can have any of the 10 digits for the last digit. So our answer is 10*10*10*10-10=9990.
中文解析:
4位数且允许重复,千位数也可以是0, 共有: 10*10*10*10=10000个. 其中以911开头的数字,其个位数可以是0-9的任意数字,因此有10个. 因此允许做密码的有: 10000-10=9990个. 答案是D.

Answer: C
Solution:
Every race eliminates 5 players. The winner is decided when there is only 1 runner left. Thus, 215 players have to be eliminated. Therefore, we need 215/5=43 games to decide the winner.
中文解析:
因为有6个赛道,因此一次比赛能淘汰5个人. 要决出冠军,需要淘汰掉215人, 215/5=43次比赛. 答案是C.

Answer: E
Solution:
10000/25=400. 400 is the 13th consecutive even integer. The largest is 400+2*12=424.
中文解析:
25个连续的偶数, 和是10,000, 则其平均数是: 10,000/25=400. 因为是连续的,因此中位数是400. 比400大的有12个数, 最大的那个数是: 400+12*2=424. 答案是E.

Answer: A
Solution:
We wish to find possible values of a,b,c. By finding the greatest common factor of 12 and 15, algebraically, it's some multiple of b and from looking at the numbers, we are sure that it is 3, thus b is 3. Moving on to a and c, in order to minimize them, a=4, c=5. Thus ,the LCM (4,5)=20.
中文解析:
a和b的最小公倍数是12. b和c的最小公倍数是15. 12 和15 都是b 的倍数, 12 和15 都是3的倍数, 则b 是3. 因此, a是4, c是5. 则a, c的最小公倍数是20.

Answer: B
Solution:
Assume that after you draw the three red chips in a row without drawing both green chips, you continue drawing for the next turn. The last/fifth chip that is drawn must be a green chip. So technically, the problem is asking for the probability that the "fifth draw" is a green chip. This probability is symmetric to the probability that the first chip drawn is green, which is 2/5.
中文解析:
结束时,取出了3个红色的,或者是2个绿色的. 如果结束时取出了3个红色的, 则5个一定还没有取完,如果我们继续取, 第5个一定是绿色的. 因此,这道题也可以理解为,第五个取出的一定是绿色的概率. 该概率是2/5. 答案是B.
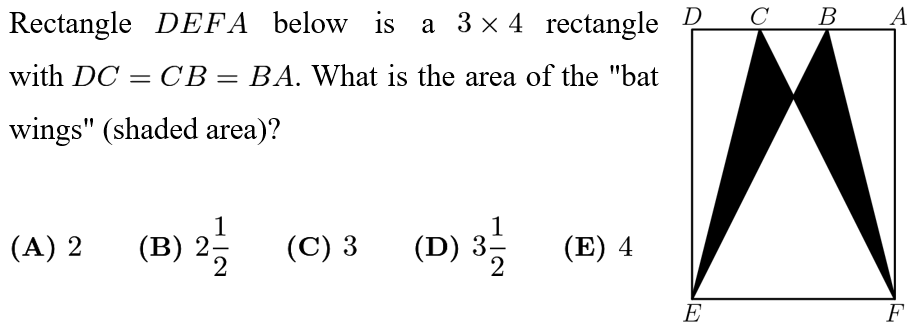
Answer: C
Solution:
The area of trapezoid CBEF is (1+3)*4/2=8. Next, we find the height of each triangle to calculate their area. The triangles are similar, and are in a 3:1 ratio , so the height of the larger one is 3 while the height of the smaller one is 1. Thus, their areas are 1/2 and 9/2. Subtracting these areas from the trapezoid, we get 8-1/2-9/2=3.
中文解析:
为了求出阴影部分的面积,我们也可以相反地,先求出白色部分的面积. 假设CF和BE相交于O点.
DE=4, DC=CB=BA=1. 长方形ADEF的面积是: 4*3=12.
三角形DCE的面积是: 1/2 * 4*1=2.
三角形ABF的面积是: 1/2 *4*1=2.
三角形CBO和三角形EFO相似, CB : EF =1: 3, 因此这两个三角形的高的比值也是1:3. 这两个三角形的高的和是4,因此高分别是1和3. 三角形CBO的面积是: 1/2 * 1* 1=0.5. 三角形EFO的面积是: 1/2 * 3*3=4.5.
所求阴影部分的面积是: 12-2-2-0.5-4.5=3. 答案是C.

Answer: C
Solution:
The two circles intersect at two points, one of which is E, let the other is F. Triangle ECF is equilateral. Thus <CEF=60. In the same way, < FED=60. <CED=<CEF+<FED=60+60=120.
中文解析:
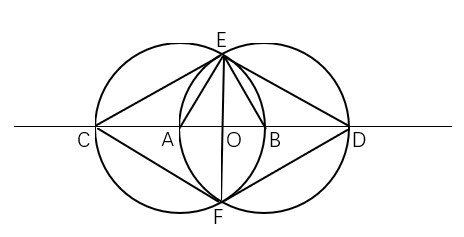
假设圆的半径是r, 则AE=r, AB=r, A0=1/2* r . 在直角三角形AOE中, AO是AE的一半, 因此角AEO 是30°. 则角EAO是60°. 角EAC=180-60=120°. 由于AE和AC都是半径, AC=AE ,且角EAC=120, 因此在等腰三角形CAE中, 角CEA=(180-120)/2=30°. 角CEO=<CEA+<AEO=30+30=60°. 由于对称性, <OED也是60°, 因此<CED=60+60=120°. 答案是C.

Answer: A
Solution:
We see that since QRS is divisible by 5, S must be 5. We notice that since PQR must be even, R must be either 2 or 4. When R=2, since RST is divisible by 3, T should be 2, 5 which cannot happen because 2 and 5 are already used up; so R=4. This gives T=3 Now, we see that Q could be either 1 or 2, but 14 is not divisible by 4, but 24 is. This means that Q=2 and P=1.
中文解析:
QRS能被5整除,因此S是5. PQR能被4整除,因此QR能被4整除, 同时R是双数,只能是2或者4. 如果R=2, R+S+T=2+5+T, 是3的倍数,因此T是2 或者5. 由于2 和5 都已经被使用了,不符合这五个字母不相等的原则, 因此R不能是2. 如果R=4, R+S+T=4+5+T, 是3的倍数,因此T=3. 既然R=4, QR能被4整除,因此Q必须是2. 剩下的P就是1. 答案是A.

Answer: B
Solution:
First, we draw a line perpendicular to the base of the triangle and cut the triangle in half. The base of the resulting right triangle would be 8, and the height would be 15. Using the Pythagorean theorem, we can find the length of the hypotenuse, which would be 17. Using the two legs of the right angle, we can find the area of the right triangle, 60. Let the radius is r. if we use the hypotenuse as base, radius as height, the area of the right triangle is 1/2 * 17 * r=60. Solving it get r=120/17.
中文解析:
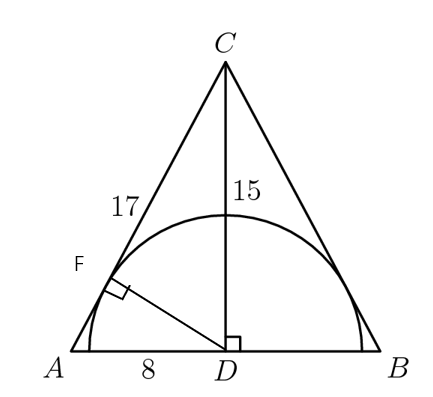
如上图所示: AD是三角形ABC的高. 在直角三角形ADC中, 根据勾股定理, 斜边AC=17. 在直角三角形ADC中, AD是低, CD是高, 其面积是1/2 * 8*15. 另一个角度看直角三角形ADC,其底是AC,高是DF. 其面积是1/2 * 17 *DF. 得到等式1/2 * 8*15=1/2 * 17* DF. 求得DF =120/17. DF 就是圆的半径,因此答案是B.
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,